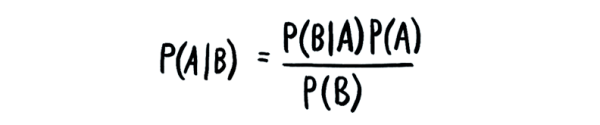Poker Room
Comparazione Bonus
-
RoomBonus
Ultime notizie
Video consigliati
La matematica del poker: il Teorema di Bayes abbinato alle carte
Area
Uno dei principi più elementari e importanti della teoria delle probabilità è il Teorema di Bayes, che prende il nome dal matematico inglese del settecento Thomas Bayes.
E’ ovvio quindi che questo teorema possa rientrare in gioco anche quando dobbiamo affrontare delle situazioni comune nelle nostre scelte al tavolo da poker.
Il Teorema di Bayes viene impiegato per calcolare la probabilità di una causa che ha scatenato l’evento che andiamo a prendere in considerazione.
Facciamo un esempio per capire meglio questa teoria: poniamo di aver fatto un test per una malattia che affligge una persona su 100 e che tale test sia accurato nel 95% dei casi e di aver ottenuto un risultato positivo da tale test.
Qual è la possibilità che in realtà non abbiamo contratto la malattia in questione?
Avete risposto il 5%? O il 99%?
In realtà se vogliamo calcolare la probabilità che una persona non soffra di una malattia per cui ha eseguito un test diagnostico, qualora tale test risulti positivo, potremmo farlo usando il Teorema di Bayes e conoscendo la frequenza con cui si presenta tale malattia (l’1% nel nostro caso) e la percentuale di efficacia del test diagnostico (il 95% nel nostro esempio).
Per comprendere come arrivare alla soluzione procediamo con la logica e vediamo come su un totale di 10.000 persone, 100 hanno la malattia (una persona su 100) e 9.900 non ce l’hanno.
Se procediamo a fare il test alle 100 con la malattia il 95% mostrerà un esito positivo al test (accurato nel 95% dei casi) e in 5 si riscontrerà esito negativo.
Allo stesso modo se procediamo a fare il test sulle 9.900 persone non malate avremo comunque il 5% di esiti positivi al test, cioè 495 persone.
Il totale delle persone positive al test, tra cui rientriamo visto l’esito positivo del nostro test, sarà quindi di 590 (95 veri malati e 495 falsi positivi). Di questi però solo 95 sono malati e quindi dividendo 95/590 troveremo la percentuale che effettivamente anche noi avremo contratto la malattia, ovvero il 16,1 %. Ben 84 volte su 100 saremo semplicemente un falso positivo.
Questa è la formula estesa per il calcolo:
Un risultato sorprendente ma come tutto questo si applica al poker?
Poniamo di trovarci davanti a una situazione definitiva, cioè che non comporti altre scelte future, come un call o un fold al river nel cash game.
Il nostro avversario punta 500 € su un piatto da 800 € su un board dove il nostro avversario punta in maniera polarizzata, quale può essere A 3
3 T
T 7
7 2
2 .
.
Il nostro avversario o ha colore e ci batte o ha una mano inferiore alla nostra visto il nostro set di dieci e visto che non può avere coppia di assi avendo semplicemente chiamato la nostra 3bet.
Scartiamo l’ipotesi che possa puntare con una mano inferiore alla nostra.
Quante volte dovrà bluffare per rendere positivo un nostro call?
Generalmente prendiamo in considerazione le pot odds dateci dalla puntata del nostro avversario e facendo 500 (l’importo puntato) / 1.800 (l’importo che vinceremmo) scopriamo che abbiamo pot odds del 28%.
Ciò significa che il nostro avversario dovrebbe bluffare 1 volta su 4 per rendere efficace il nostro call.
Se pensiamo che il nostro avversario punti in bluff un numero minore di volte il nostro call diventa negativo.
Oltre a questo però è bene prendere in considerazione un altro parametro come appena insegnatoci dal Teorema di Bayes: quante combinazioni di mani potrebbe avere il nostro avversario.
Nell’esempio sopra riportato il nostro avversario potrebbe avere 20 combinazioni di colore.
Ma quale è invece il numero delle combinazioni con il quale è arrivato al river?
Poniamo che siano un totale di 100 combinazioni per comodità, delle quali 20 sono i colori, 30 sono mani che decidono di non puntare e 50 sono combinazioni che il nostro avversario potrebbe puntare in bluff.
Facile sarà quindi capire che dovendo arrivare al 28% per giustificare il nostro call, l’avversario dovrà bluffare almeno con 8 delle 50 combinazioni di bluff, infatti 8/28 (le 20 combinazioni di colore più gli 8 bluff) è uguale al 28,6%, numero superiore al 28% necessario per il call.
Quindi in definitiva il nostro avversario dovrà bettare con almeno 8 delle 50 combinazioni di bluff, cioè almeno il 16% delle volte.
A questo punto dovremo infine domandarci se abbiamo di fronte un oppo che bluffa almeno il 16% delle volte che ne ha la possibilità oppure è un giocatore più nitty.
La percentuale trovata è decisamente inferiore a quella volta su 4 che avremmo preso in considerazione senza tenere presente il Teorema di Bayes.
L’importante è stabilire adeguatamente il range dell’avversario e il numero di combo che può avere in modo da identificare correttamente i campioni da considerare.